Pada topik-topik sebelumnya, kalian telah banyak belajar mengenai vektor. Nah, pada topik kali ini kalian akan belajar tentang penggunaan kaidah vektor dalam menyelesaikan masalah nyata, terutama masalah fisika.
Coba sebutkan beberapa contoh masalah fisika yang menggunakan vektor.
Tepat sekali. Perpindahan, resultan gaya yang bekerja pada suatu benda, resultan perpindahan, dan kesetimbangan merupakan beberapa contoh masalah fisika yang menggunakan vektor.
Nah, untuk memudahkan kalian dalam memahami materi ini, yuk kita cermati beberapa contoh soal berikut.
P sejauh 10 km ke dermaga A yang berada di arah utara. Selanjutnya perahu itu berlayar sejauh 14 km ke arah timur menuju dermaga B . Setelah beberapa menit, perahu tersebut kembali berlayar sejauh 8 km ke arah barat daya menuju dermaga C . Tentukan resultan perpindahan perahu layar tersebut.
Penyelesaian:
Permasalahan dalam soal dapat diselesaikan dengan cara membuat sketsa. Nah, dalam membuat sketsa, kalian perlu menggunakan skala, busur derajat, dan kompas sebagai penunjuk arah utara (koordinat 000°).
Jika dalam sketsa yang akan kita buat dimisalkan jarak 1 cm mewakili jarak 1 km, maka sketsa tersebut adalah sebagai berikut:
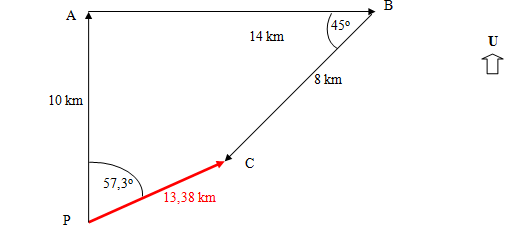
Pada sketsa di atas, tampak bahwa resultan perpindahan perahu layar sama dengan panjang vektorPC−→−− .
Nah, jika kita ukur dengan penggaris, ternyata panjang vektorPC−→−− adalah 13,38 cm dan ∠APC=57,3° .
Dengan demikian, dapat kita simpulkan bahwa perpindahan yang dilakukan oleh perahu layar adalah sejauh 13,38 km dengan arah 057,3°.
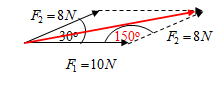
F1=10 N bekerja pada sebuah balok pada arah horizontal. Jika gaya lain yang bekerja pada balok adalah sebesar F2=8 N dan besar sudut antara kedua gaya adalah 30°, maka berapakah resultan gaya yang bekerja pada balok?
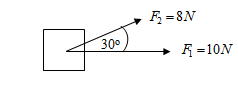
Penyelesaian:
Jika kita misalkan jarak 1 cm mewakili gaya sebesar 1 N, maka sketsa dari permasalahan dalam soal di atas adalah sebagai berikut:
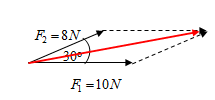
Pada sketsa di atas, vektor yang berwarna merah merupakan resultan dua gaya yang bekerja pada balok.
Nah, untuk menentukan besar resultan gaya, kalian perlu mengukur panjang vektor yang berwarna merah.
Jika sketsa yang kalian buat sudah presisi, maka panjang vektor berwarna merah adalah 17,4 cm. Dengan kata lain, besar resultan gaya pada balok adalah 17,4 N, dimana besar sudut antara vektor resultan dan vektor yang mewakiliF1 adalah 13,29°.
Perlu kalian ketahui bahwa resultan gaya pada contoh 2 juga dapat dihitung dengan menggunakan rumus.
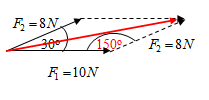
R===F12+F22+2×F1×F2×cos30°−−−−−−−−−−−−−−−−−−−−−−−−−−−√102+82+2×10×8×123√−−−−−−−−−−−−−−−−−−−−−−−√17,4
atau
R====F12+F22−2×F1×F2×cos150o−−−−−−−−−−−−−−−−−−−−−−−−−−−−√102+82−2×10×8×(−123√)−−−−−−−−−−−−−−−−−−−−−−−−−−√164+803√−−−−−−−−−√17,4
Lantas bagaimanakah cara menghitung besar sudut antara gaya pada arah horizontal dengan resultannya?
Ya, tentu saja dengan menggunakan perbandingan trigonometri sinus.
sinθ8⇔sinθ⇔θ====sin150°17,48sin150°17,40,229813,29°
Berdasarkan uraian di atas, dapat disimpulkan bahwa besar sudut antara vektor yang mewakili gayaF1 dan vektor resultan adalah 13,29°.
Yuk kita cermati contoh soal berikutnya.
θ . Uraikan komponen gaya yang bekerja pada balok tersebut.
Penyelesaian:
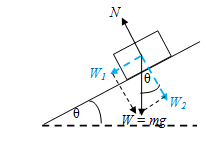
Gaya yang bekerja pada balok adalah
W2 sama dengan besar gaya normal N .
Perlu kalian ketahui, apabila terdapat ketidakseimbangan pada komponen yang sejajar dengan bidang miring, maka balok dapat meluncur turun pada bidang miring.
Apakah kalian sudah paham dengan materi di atas?
Coba sebutkan beberapa contoh masalah fisika yang menggunakan vektor.
Tepat sekali. Perpindahan, resultan gaya yang bekerja pada suatu benda, resultan perpindahan, dan kesetimbangan merupakan beberapa contoh masalah fisika yang menggunakan vektor.
Nah, untuk memudahkan kalian dalam memahami materi ini, yuk kita cermati beberapa contoh soal berikut.
Contoh 1
Penyelesaian:
Permasalahan dalam soal dapat diselesaikan dengan cara membuat sketsa. Nah, dalam membuat sketsa, kalian perlu menggunakan skala, busur derajat, dan kompas sebagai penunjuk arah utara (koordinat 000°).
Jika dalam sketsa yang akan kita buat dimisalkan jarak 1 cm mewakili jarak 1 km, maka sketsa tersebut adalah sebagai berikut:

Pada sketsa di atas, tampak bahwa resultan perpindahan perahu layar sama dengan panjang vektor
Nah, jika kita ukur dengan penggaris, ternyata panjang vektor
Dengan demikian, dapat kita simpulkan bahwa perpindahan yang dilakukan oleh perahu layar adalah sejauh 13,38 km dengan arah 057,3°.
Contoh 2

Penyelesaian:
Jika kita misalkan jarak 1 cm mewakili gaya sebesar 1 N, maka sketsa dari permasalahan dalam soal di atas adalah sebagai berikut:

Pada sketsa di atas, vektor yang berwarna merah merupakan resultan dua gaya yang bekerja pada balok.
Nah, untuk menentukan besar resultan gaya, kalian perlu mengukur panjang vektor yang berwarna merah.
Jika sketsa yang kalian buat sudah presisi, maka panjang vektor berwarna merah adalah 17,4 cm. Dengan kata lain, besar resultan gaya pada balok adalah 17,4 N, dimana besar sudut antara vektor resultan dan vektor yang mewakili
Perlu kalian ketahui bahwa resultan gaya pada contoh 2 juga dapat dihitung dengan menggunakan rumus.

atau
Lantas bagaimanakah cara menghitung besar sudut antara gaya pada arah horizontal dengan resultannya?
Ya, tentu saja dengan menggunakan perbandingan trigonometri sinus.

Berdasarkan uraian di atas, dapat disimpulkan bahwa besar sudut antara vektor yang mewakili gaya
Yuk kita cermati contoh soal berikutnya.
Contoh 3
Penyelesaian:

Gaya yang bekerja pada balok adalah
- berat benda
→W=m×g , dimanam adalah massa balok dang adalah gaya grafitasi - gaya normal
N
→ gaya ini mengarah keluar terhadap permukaan blok - gaya yang sejajar dengan permukaan bidang miring →
W1 - gaya yang tegak lurus dengan permukaan bidang miring →
W2
W1=m×g×sinθ W2=m×g×cosθ
Perlu kalian ketahui, apabila terdapat ketidakseimbangan pada komponen yang sejajar dengan bidang miring, maka balok dapat meluncur turun pada bidang miring.
Apakah kalian sudah paham dengan materi di atas?




0 komentar:
Posting Komentar