Ingat kembali bahwa matriks nol dan matriks identitas, berturut-turut mempunyai determinan 0 dan 1. Kita dapat mencari nilai determinan jika dan hanya jika matriks tersebut adalah matriks bujur sangkar. Adapun yang menentukan kesingularan dari matriks bujur sangkar adalah nilai determinannya.
Dalam pelajaran ini, kalian akan belajar tentang bagaimana untuk :
- Menentukan kesingularan sebuah matriks
- Menemukan matriks invers dari sebuah matriks berukuran 2x2 atau 3x3.
Kita dapat memeriksa apakah sebuah matriks mempunyai invers atau tidak dengan cara menghitung determinannya. Jika determinan matriks bujur sangkar tersebut tidak sama dengan nol, maka matriks tersebut mempunyai invers terhadap operasi perkalian.
Lalu, bagaimanakah dengan kesingularan matriks? Jika sebuag matriks tidak mempunyai invers, maka matriks tersebut disebut sebagai matriks singular. Adapun, matriks singular biasa disebut sebagaimatriks degenerate.
Sebuah matriks mempunyai invers jika matriks tersebut :
- Merupakan matriksbujur sangkar, sehingga kita dapat mencari determinannya
- Merupakan matriksnon singular, sehingga determinannya tidak sama dengan nol
Dua buah matriks dikatakan saling invers terhadap operasi perkalianjika hasil perkalian kedua matriks tersebut adalah matriks identitas.
Diberikan matriks A dan B, dimana keduanya adalah matriks bujur sangkar dan matriks non singular.
Jika A.B = I, maka B dikatakan sebagai invers dari A dan A disebut sebagai invers dari B. Matriks A dan B tentunya mempunyai ukuran yang sama.
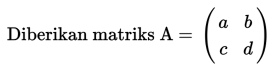
Kita dapat mencari matriks invers dengan cara sebagai berikut :
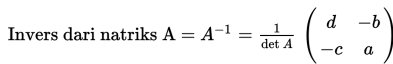
Selanjutnya, untuk mencari invers dari matriks berukuran 3x3, kita membutuhkan langkah yang lebih banyak. Pertama-tama, kita harus mencari semua Minor dan Kofaktor.
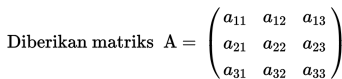
Minor dari elemen a ij dibentuk dengan cara menghitung determinan dari matriks yang diperoleh dengan cara menghapus baris ke-i dan kolom ke- j.
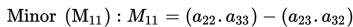
Kofaktor dari elemenij dibentuk dengan menggunakan minor Mij dan menerapkan persamaan berikut ini :
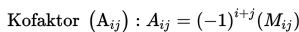
Adjoin dari sebuah matriks terdiri atas kofaktor-kofaktor.
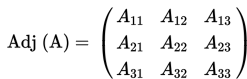
Untuk matriks 3x3, kita dapat mencari inversnya dengan menggunakan persamaan berikut ini :
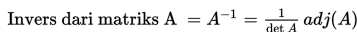
Sebuah matriks transpos dibentuk dengan cara saling menukarkan baris dan kolom dari matriks awal.
Matriks transpos dari matriks A dilambangkan dengan : AT
Berikut ini adalah beberapa sifat matriks invers :
- (AB)-1 = B-1 A-1
- (AT)-1 = (A-1)T )-1 = (A-1)T
- (A-1)-1 = A
Contoh 1 :
Dari pilihan berikut ini, manakah yang merupakan matriks singular?
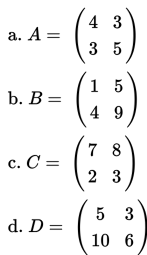
Penjelasan :
Sebuah matriks, dikatakan singular jika determinannya sama dengan nol. Selanjutnya, karena matriks D pada contoh di atas mempunyai determinan nol, maka D adalah matriks singular.
Opsi D adalah jawaban yang benar.
Contoh 2 :
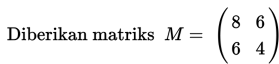
Dari pilihan berikut ini, manakah yang merupakan matriks invers dari matriks M?
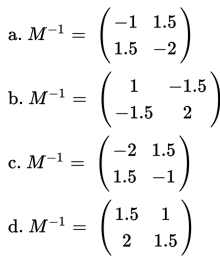
Penjelasan :
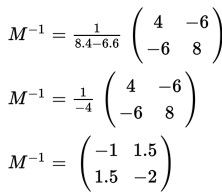
Opsi A adalah jawaban yang benar.
Sekian pembahasan... sampai bertemu di postingan berikutnya.....
Sekian pembahasan... sampai bertemu di postingan berikutnya.....




0 komentar:
Posting Komentar