Mari simak ilustrasi berikut.
Untuk menggiring bola, pemain sepak bola memberikan gaya pada bola agar bola berpindah ke posisi yang dikehendaki. Gaya merupakan salah satu besaran vektor. Ini berarti, dalam proses tersebut pemain telah melakukan operasi matematika pada bola, yaitu menambahkan dan mengurangkan vektor gaya pada bola.

Sumber gambar: dokumen pribadi
Seperti halnya besaran lainnya, operasi matematika juga dapat dilakukan pada vektor diantaranya adalah penjumlahan dan pengurangan. Ada dua pendekatan yang digunakan untuk menentukan hasil operasi penjumlahan dan pengurangan vektor yaitu pendekatan grafis dan pendekatan matematis.
Misalkan terdapat dua yaitu vektorA−→danB−→ yang digambarkan sebagai ruas garis berarah seperti di bawah ini.
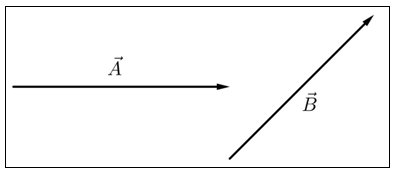
Hasil penjumlahan dan pengurangan vektor di atas dapat ditentukan dengan beberapa pendekatan salah satunya pendekatan grafis. Ada dua macam pendekatan grafis yang dapat digunakan untuk menentukan hasil operasi penjumlahan dan pengurangan vektor yaitu metode ujung ke pangkal (tip-to-tail method) dan metode jajargenjang.
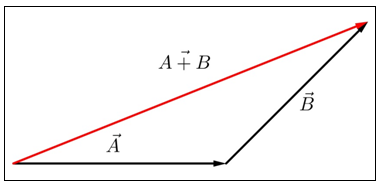
(A−→+B−→) , kita cukup menggeser salah satu vektor menuju vektor lainnya, sedemikian sehingga ujung (tip) salah satu vektor berimpit dengan pangkal (tail) vektor lainnya. Hasil penjumlahan (resultan) kedua vektor tersebut digambarkan sebagai berikut.
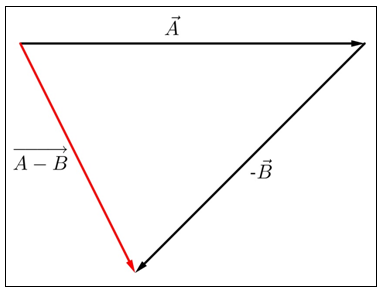
Untuk mengurangkan kedua vektor misalnyaA−→−B−→ , kita dapat memanfaatkan prinsip aljabar yaitu a - b = a + (-b). Ini berarti, kita cukup membalik arah vektor B−→ menjadi −B−→−− (invers penjumlahan vektor). Kemudian, gunakan metode tip-to-tail seperti halnya operasi penjumlahan vektor. Hasil pengurangan kedua vektor tersebut digambarkan seperti di bawah ini.
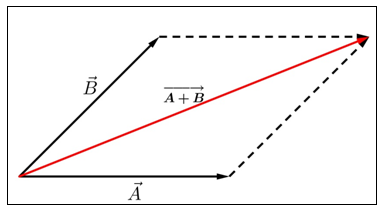
(A−→+B−→) merupakan diagonal jajargenjang yang dilukis dari titik pangkal vektor yang berimpit. Resultan vektor tersebut digambarkan sebagai berikut.
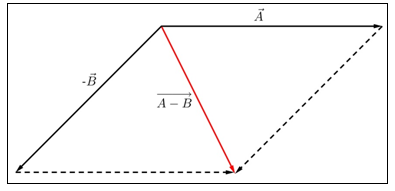
Untuk mengurangkanA−→ dengan B−→ , langkah awalnya sama dengan metode tip-to-tail, yaitu membalik arah vektor B−→ menjadi −B−→ . Langkah selanjutnya adalah menggeser A−→dan−B−→ agar pangkalnya berimpit. Terakhir, lengkapi gambar menjadi jajargenjang dengan menambahkan sisi yang sejajar dengan masing-masing vektor. Hasil pengurangan kedua vektor tersebut yang merupakan diagonal jajargenjang yaitu:
Modifikasi kedua metode ini dapat diterapkan untuk operasi yang melibatkan lebih dari dua vektor di ruang dimensi 2 atau 3 seperti:
A−→+B−→+C−→+D−→+E−→+F−→+...=(A−→+B−→)+(C−→+D−→)+(E−→+F−→)+...
dan
A−→−B−→−C−→−D−→−E−→−F−→−...=(A−→−B−→)−(C−→+D−→)−(E−→+F−→)−...
Dengan kata lain, kamu cukup mengulang penjumlahan untuk setiap dua vektor secara terpisah.
Misalkan dua buah vektor dinyatakan dalam komponen pembentuknya berupaA−→=⟨a1,a2⟩danB−→=⟨b1,b2⟩ , sehingga operasi penjumlahan dan pengurangan kedua vektor ini dapat didefinisikan sebagai berikut.
A−→+B−→=⟨a1,a2⟩+⟨b1,b2⟩=⟨a1+b1,a2+b2⟩
A−→−B−→=⟨a1,a2⟩−⟨b1,b2⟩=⟨a1−b1,a2−b2⟩
Seperti halnya pendekatan grafis, pendekatan matematis juga dapat dimodifikasi untuk menghitung penjumlahan dan pengurangan yang melibatkan lebih dari dua vektor sebagai berikut.
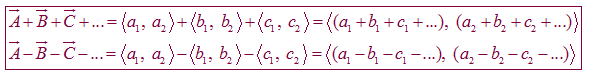
Kelebihan dari pendekatan matematis adalah kita tidak harus menggambarkan vektor-vektor yang terlibat dalam perhitungan. Ini karena vektor-vektor yang memiliki dimensi lebih dari 3 tidak dapat digambarkan di atas kertas, sehingga pendekatan matematis berikut akan sangat berguna untuk operasi penjumlahan dan pengurangan di ruang dimensi n.
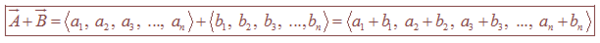
OA−→−−=⟨ax,ay⟩ pada koordinat Cartesius berikut ini. Misalkan vektor tersebut membentuk sudut θ terhadap sumbu x.
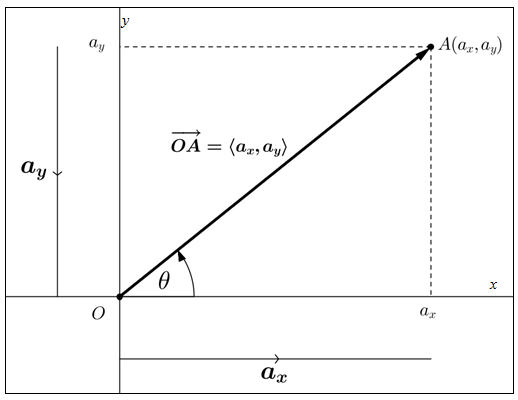
Berdasarkan gambar di atas, panjang vektorOA−→−−=⟨ax,ay⟩ dapat dihitung dengan memanfaatkan dalil Pythagoras yaitu:
∣∣OA−→−−∣∣=ax2+ay2−−−−−−−−√ .
Besar sudut θ dapat dihitung dengan mengambil invers dari fungsi tangen sudutnya yaitu:
tanθ=ayax
⇔θ=tan−1(ayax)
Perhatikan gambar vektorOP−→−−=⟨px,py,pz⟩ pada ruang dimensi tiga berikut.
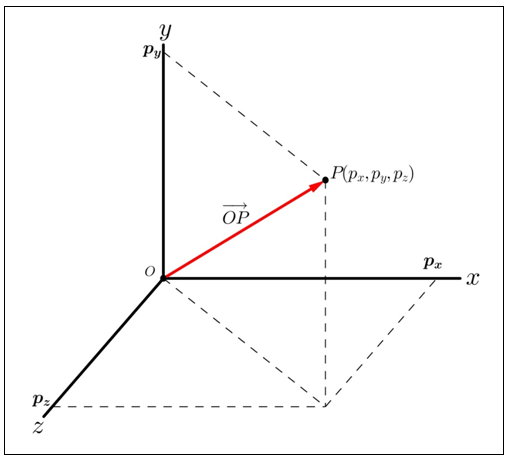
Panjang vektorOP−→−−=⟨px,py,pz⟩ adalah:
∣∣OP−→−−∣∣=px2+py2+pz2−−−−−−−−−−−−√ ,
sedangkan panjang vektorN−→=⟨n1,n2,n3,...,nn⟩ yang berdimensi n dapat dihitung dengan rumus:
∣∣N−→∣∣=n21+n22+n23+...+n2n−−−−−−−−−−−−−−−−−√
Diketahui vektorA−→,B−→,danC−→ sebagai berikut.
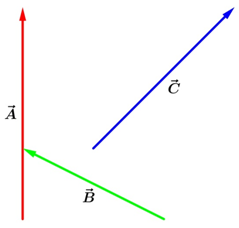
Tentukan gambaran vektorA−→+B−→−C−→ berdasarkan pendekatan grafis.
Penyelesaian:
Metode yang digunakan adalah metode tip-to-tail.
Mula-mula, gambarkan vektorA−→+B−→ .
Selanjutnya, geser pangkal vektor−C−→ agar berimpit di ujung resultan A−→+B−→ , sehingga diperoleh:
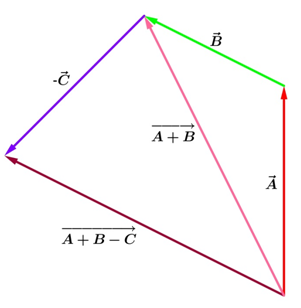
Diketahui vektorA−→=⟨1,2,3⟩,B−→=⟨1,0,−1⟩,danC−→=⟨−3,2,−4⟩ . Tentukan komponen vektor A−→+B−→−C−→ .
Penyelesaian:
Penjumlahan vektor tersebut dapat dilakukan dengan mengoperasikan komponen-komponen yang bersesuaian dari setiap vektor sebagai berikut.
A−→+B−→−C−→=⟨1,2,3⟩+⟨1,0,−1⟩−⟨−3,2,−4⟩
⇔A−→+B−→−C−→=⟨(1+1−(−3)),(2+0−2),(3+(−1)−(−4))⟩
⇔A−→+B−→−C−→=⟨5,0,6⟩
Jadi,A−→+B−→−C−→=⟨5,0,6⟩ .
Tentukan panjang dari vektorP−→=⟨5,0,6⟩ .
Penyelesaian:
Dengan menggunakan rumus panjang vektor di peroleh:
∣∣P−→∣∣=52+02+62−−−−−−−−−−√
⇔∣∣P−→∣∣=25+0+36−−−−−−−−−√
⇔∣∣P−→∣∣=61−−√
Jadi,∣∣P−→∣∣=61−−√ satuan.
Perhatikan diagram vektor berikut.
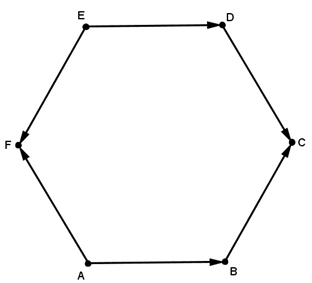
Gambarkan vektorAB−→−−+BC−→−−+DC−→−−+ED−→−−+EF−→−−+AF−→−− berdasarkan pendekatan grafis.
Penyelesaian:
Permasalahan ini dapat kita sederhanakan dengan mengelompokkan vektor-vektor yang diketahui.
Perhatikan gambar berikut.
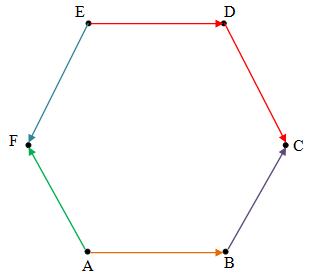
Berdasarkan gambar di atas, vektor-vektor dikelompokkan menjadi:
AB−→−−+BC−→−−+AF−→−−+EF−→−−+(DC−→−−+ED−→−−) .
Ingat bahwa, setiap vektor dapat digeser tanpa mengubah panjang dan arahnya.
Salah satu contoh gambaran yang diperoleh dengan menggunakan metode tip-to-tail adalah sebagai berikut.
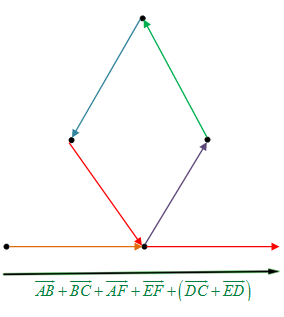
Apakah kamu sudah paham dengan penjelasan di atas? Ayo tingkatkan pemahamanmu dengan mengerjakan soal-soal. Selamat belajar.
Untuk menggiring bola, pemain sepak bola memberikan gaya pada bola agar bola berpindah ke posisi yang dikehendaki. Gaya merupakan salah satu besaran vektor. Ini berarti, dalam proses tersebut pemain telah melakukan operasi matematika pada bola, yaitu menambahkan dan mengurangkan vektor gaya pada bola.

Sumber gambar: dokumen pribadi
Seperti halnya besaran lainnya, operasi matematika juga dapat dilakukan pada vektor diantaranya adalah penjumlahan dan pengurangan. Ada dua pendekatan yang digunakan untuk menentukan hasil operasi penjumlahan dan pengurangan vektor yaitu pendekatan grafis dan pendekatan matematis.
Pendekatan Grafis
Prinsip dasar pendekatan grafis pada operasi vektor adalah vektor tidak berubah jika posisinya digeser tanpa mengubah panjang dan arahnya. Mari simak penjelasan berikut agar kamu lebih paham.Misalkan terdapat dua yaitu vektor

Hasil penjumlahan dan pengurangan vektor di atas dapat ditentukan dengan beberapa pendekatan salah satunya pendekatan grafis. Ada dua macam pendekatan grafis yang dapat digunakan untuk menentukan hasil operasi penjumlahan dan pengurangan vektor yaitu metode ujung ke pangkal (tip-to-tail method) dan metode jajargenjang.
Metode Ujung ke Pangkal (tip-to-tail method)
Metode ujung ke pangkal (tip-to-tail method) juga dikenal dengan metode segitiga. Untuk menjumlahkan kedua vektor yang dimaksud
Untuk mengurangkan kedua vektor misalnya

Metode Jajargenjang
Pada metode ini, kedua vektor digeser sehingga pangkal kedua vektor berimpit di satu titik, kemudian dilanjutkan dengan melengkapi gambar menjadi sebuah jajargenjang. Hasil penjumlahan (resultan) kedua vektor
Untuk mengurangkan

Modifikasi kedua metode ini dapat diterapkan untuk operasi yang melibatkan lebih dari dua vektor di ruang dimensi 2 atau 3 seperti:
dan
Dengan kata lain, kamu cukup mengulang penjumlahan untuk setiap dua vektor secara terpisah.
Pendekatan Matematis
Pendekatan matematis dapat dipandang sebagai penyempurnaan pendekatan grafis. Prinsip dasar yang digunakan adalah menyatakan setiap vektor ke dalam komponen-komponen pembentuknya. Mari kita mulai dari suatu kasus umum pada ruang dimensi dua (R2 ).Misalkan dua buah vektor dinyatakan dalam komponen pembentuknya berupa
Seperti halnya pendekatan grafis, pendekatan matematis juga dapat dimodifikasi untuk menghitung penjumlahan dan pengurangan yang melibatkan lebih dari dua vektor sebagai berikut.
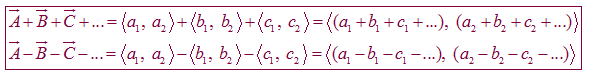
Kelebihan dari pendekatan matematis adalah kita tidak harus menggambarkan vektor-vektor yang terlibat dalam perhitungan. Ini karena vektor-vektor yang memiliki dimensi lebih dari 3 tidak dapat digambarkan di atas kertas, sehingga pendekatan matematis berikut akan sangat berguna untuk operasi penjumlahan dan pengurangan di ruang dimensi n.
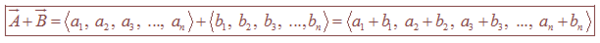
Lebih Jauh tentang Panjang Vektor
Perhatikan vektor dua dimensi
Berdasarkan gambar di atas, panjang vektor
Besar sudut θ dapat dihitung dengan mengambil invers dari fungsi tangen sudutnya yaitu:
Perhatikan gambar vektor

Panjang vektor
sedangkan panjang vektor
✎Contoh 1
Diketahui vektor

Tentukan gambaran vektor
Penyelesaian:
Metode yang digunakan adalah metode tip-to-tail.
Mula-mula, gambarkan vektor
Selanjutnya, geser pangkal vektor

✎Contoh 2
Diketahui vektor
Penyelesaian:
Penjumlahan vektor tersebut dapat dilakukan dengan mengoperasikan komponen-komponen yang bersesuaian dari setiap vektor sebagai berikut.
Jadi,
✎Contoh 3
Tentukan panjang dari vektor
Penyelesaian:
Dengan menggunakan rumus panjang vektor di peroleh:
Jadi,
✎Contoh 4
Perhatikan diagram vektor berikut.

Gambarkan vektor
Penyelesaian:
Permasalahan ini dapat kita sederhanakan dengan mengelompokkan vektor-vektor yang diketahui.
Perhatikan gambar berikut.

Berdasarkan gambar di atas, vektor-vektor dikelompokkan menjadi:
Ingat bahwa, setiap vektor dapat digeser tanpa mengubah panjang dan arahnya.
Salah satu contoh gambaran yang diperoleh dengan menggunakan metode tip-to-tail adalah sebagai berikut.

Poin Penting
- Secara grafis, penjumlahan dan pengurangan vektor dilakukan dengan metode tip-to-tail dan jajargenjang.
- Secara matematis, penjumlahan dan pengurangan vektor dilakukan dengan mengoperasikan komponen-komponen yang bersesuaian dari masing-masing vektor.
- Panjang vektor
N−→=⟨n1,n2,n3,...,nn⟩ adalah∣∣N−→∣∣=n21+n22+n23+...+n2n−−−−−−−−−−−−−−−−−√ . - Untuk sebarang vektor
OA−→−−=⟨ax–0,ay−0⟩ , besar sudut θ yang dibentuk oleh vektor dengan sumbu x ditentukan dengan menggunakan invers dari fungsi tangen sudut.θ=tan−1(ayax)
Apakah kamu sudah paham dengan penjelasan di atas? Ayo tingkatkan pemahamanmu dengan mengerjakan soal-soal. Selamat belajar.




0 komentar:
Posting Komentar