Perkalian Silang antara Dua Vektor (Cross Product)

Pada topik sebelumnya kalian telah belajar tentang perkalian titik antara dua vektor (dot product). Nah, pada topik kali ini kalian akan belajar mengenai perkalian silang antara dua vektor (cross product).
Tentu kalian pernah mendengar istilah "cross product" dalam mata pelajaran Fisika bukan?
Dalam Fisika, cross product biasanya diilustrasikan dengan kaidah/aturan tangan kanan.

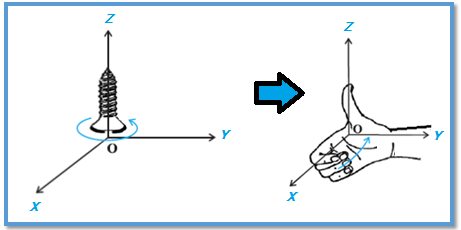
Nah, pada gambar di atas, apabila sumbu X positif diputar berlawanan arah dengan arah putar jarum jam ke arah sumbu Y positif, maka sekrup akan bergerak ke arah sumbu Z positif.
Pada kaidah/aturan tangan kanan, ibu jari menyatakan arah dari sumbu Z positif dan jari-jari yang ditekuk menyatakan arah dari sumbu X.

Definisi

Misal terdapat dua vektor tak nol, yaitu vektor a→ dan b→ dengan besar sudut antara kedua vektor adalah θ.
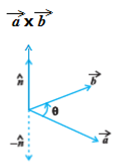
Nah, perkalian silang antara vektor a→ dan b→ adalah a→×b→=∣∣a→∣∣∣∣∣b→∣∣∣sinθ×nˆ.
Vektor nˆ pada rumus di atas adalah vektor normal, yaitu vektor satuan yang tegak lurus dengan vektor a→ dan b→.
Perlu kalian ketahui, besar sudut antara kedua vektor adalah 0≤θ≤π.

Sifat-Sifat

• antikomutatif → a→×b→=−b→×a→
• ditributif
  
  → a→×(b→+c→)=a→×b→+a→×c→
  
  → (a→+b→)×c→=a→×c→+b→×c→
• k(a→×b→)=(ka→)×b→=a→×(kb→)

Perlu kalian ketahui, vektor a→, b→, dan c→ berada di R3, sedangkan k adalah konstanta/skalar.

Tahukah kalian bagaimana sifat antikomutatif muncul?
Yuk kita cermati gambar berikut.

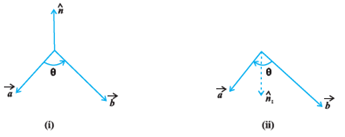
Pada gambar (i), arah putar θ adalah dari vektor a→ ke vektor b→. Adapun arah putar θ pada gambar (ii) adalah dari vektor b→ ke vektor a→.
Pada gambar di atas, tampak pula bahwa arah vektor normal n→ adalah ke atas dan arah vektor normal n1−→− adalah ke bawah → n1−→−=−n→.
Dengan demikian,
a→×b→===∣∣a→∣∣∣∣∣b→∣∣∣sinθnˆ−∣∣a→∣∣∣∣∣b→∣∣∣sinθnˆ1−b→×a→

Apakah kalian tahu apa yang terjadi jika dua buah vektor saling tegak lurus?

Dua Vektor Saling Tegak Lurus

Seperti yang telah kalian ketahui, jika dua buah vektor saling tegak lurus, maka besar sudut antara kedua vektor tersebut adalah π2 radian.
Dengan demikian,
∣∣∣a→×b→∣∣∣====∣∣a→∣∣∣∣∣b→∣∣∣sinθ∣∣a→∣∣∣∣∣b→∣∣∣sinπ2∣∣a→∣∣∣∣∣b→∣∣∣×1∣∣a→∣∣∣∣∣b→∣∣∣

Nah, apa yang akan terjadi jika dua buah vektor segaris?

Dua Vektor Segaris

Jika dua buah vektor segaris dan searah, maka besar sudut antara kedua vektor tersebut adalah 0 radian.
Dengan demikian,
∣∣∣a→×b→∣∣∣====∣∣a→∣∣∣∣∣b→∣∣∣sinθ∣∣a→∣∣∣∣∣b→∣∣∣sin(0)∣∣a→∣∣∣∣∣b→∣∣∣×00

Selanjutnya, jika dua buah vektor segaris dan berlawanan arah, maka besar sudut antara kedua vektor tersebut adalah π radian.
Dengan demikian,
∣∣∣a→×b→∣∣∣====∣∣a→∣∣∣∣∣b→∣∣∣sinθ∣∣a→∣∣∣∣∣b→∣∣∣sinπ∣∣a→∣∣∣∣∣b→∣∣∣×00

Bentuk Catesius

Seperti yang telah kalian pelajari dalam Fisika, hasil perkalian silang antara vektor basis dengan dirinya sendiri adalah nol, sebab sudut yang terbentuk adalah 0 radian.
iˆ×iˆ=jˆ×jˆ=kˆ×kˆ=0
Nah, selanjutnya karena vektor basis saling tegak lurus, maka
iˆ×jˆ=kˆjˆ×iˆ=−kˆjˆ×kˆ=iˆkˆ×jˆ=−iˆkˆ×iˆ=jˆiˆ×kˆ=−jˆ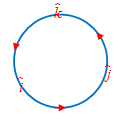


Tahukah kalian bagaimana cara menentukan cross product jika besar sudut antara kedua vektor tidak diketahui?
Misalkan a→=a1iˆ+a2jˆ+a3kˆ dan b→=b1iˆ+b2jˆ+b3kˆ.
Nah, perkalian silang antara vektor a→ dan b→ adalah sebagai berikut:
a→×b→====(a1iˆ+a2jˆ+a3kˆ)×(b1iˆ+b2jˆ+b3kˆ)a1b1(iˆ×iˆ)+a1b2(iˆ×jˆ)+a1b3(iˆ×kˆ)+a2b1(jˆ×iˆ)+a2b2(jˆ×jˆ)+a2b3(jˆ×kˆ)+a3b1(kˆ×iˆ)+a3b2(kˆ×jˆ)+a3b3(kˆ×kˆ)a1b2k→+a1b3(−j→)+a2b1(−kˆ)+a2b3(iˆ)+a3b1(jˆ)+a3b2(−iˆ)a1b2k→−a1b3j→−a2b1kˆ+a2b3iˆ+a3b1j→−a3b2i→

Sulit untuk menghafalkan bentuk di atas bukan?
Agar kalian tidak kesulitan dalam menghafalkan bentuk di atas, mari kita ubah bentuk di atas ke dalam bentuk determinan.
a→×b→=a1b2k→−a1b3j→−a2b1kˆ+a2b3iˆ+a3b1j→−a3b2i→=[a2b3iˆ−a3b2i→]+[a3b1j→−a1b3j→]+[a1b2k→−a2b1kˆ]=[a2b3−a3b2]iˆ+[a3b1−a1b3]j→+[a1b2−a2b1]k→=[a2b3−a3b2]iˆ−[a1b3−a3b1]j→+[a1b2−a2b1]k→=iˆ∣∣∣a2b2a3b3∣∣∣−jˆ∣∣∣a1b1a3b3∣∣∣+kˆ∣∣∣a1b1a2b2∣∣∣=∣∣∣∣∣iˆa1b1jˆa2b2kˆa3b3∣∣∣∣∣
Nah, sekarang kalian sudah tidak kesulitan lagi untuk menghafal rumus a→×b→ bukan?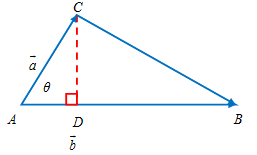

Menghitung Luas Segitiga

Untuk ∆ABC sebarang, luas segitiga tersebut dapat dihitung dengan menggunakan rumus luas segitiga, yaitu LΔABC=12∣∣AB−→−−∣∣×∣∣CD−→−−∣∣.
Nah, karena CD−→−−=AC−→−−sinθ, AC−→−−=a→, dan AB−→−−=b→, maka LΔABC=12∣∣a→∣∣∣∣∣b→∣∣∣sinθ=12∣∣∣a→×b→∣∣∣.

Luas Trapesium

Selain dapat digunakan untuk menghitung luas segitiga sebarang, perkalian silang antara dua vektor juga dapat digunakan untuk menghitung luas trapesium.

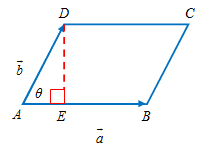Apakah kalian masih ingat dengan rumus jajargenjang?
Ya, rumus jajargenjang ABCD adalah ∣∣AB−→−−∣∣×∣∣DE−→−−∣∣.
Nah, karena DE−→−−=AB−→−−sinθ, AB−→−−=a→, dan AD−→−−=b→, maka LABCD=∣∣a→∣∣∣∣∣b→∣∣∣sinθ=∣∣∣a→×b→∣∣∣.