Vektor Satuan dan Kesamaan Dua Vektor

Dalam topik sebelumnya kalian telah belajar mengenai vektor posisi dan panjang vektor.
Apakah kalian masih ingat dengan materi tersebut?
Saya yakin kalian masih ingat.
Nah, kedua materi tersebut akan kalian gunakan untuk mempelajari topik ini.

Vektor Satuan

Vektor satuan adalah vektor dengan panjang satu satuan.

Bagaimanakah cara menentukan vektor satuan dari suatu vektor?
Misalkan a→ adalah vektor tak nol. Nah, vektor satuan yang searah dengan vektor a→ adalah vektor aˆ yang dapat ditentukan dengan menggunakan rumus: aˆ=a→∣∣a→∣∣.


Perlu kalian ketahui, vektor satuan dalam sistem koordinat dinyatakan dalam bentuk vektor basis, yaitu:

• vektor iˆ → vektor satuan pada arah sumbu X
• vektor jˆ → vektor satuan pada arah sumbu Y
• vektor kˆ → vektor satuan pada arah sumbu Z

Coba tebak, bagaimanakah elemen dari vektor basis di R2 dan R3?
Pada R2, hanya ada dua vektor basis, yaitu iˆ=(10 ) dan jˆ=(01 ).
Nah, vektor basis di R3 ada tiga, yaitu iˆ=⎛⎝⎜100 ⎞⎠⎟, jˆ=⎛⎝⎜010 ⎞⎠⎟, dan kˆ=⎛⎝⎜001 ⎞⎠⎟.
Jika kalian hitung, panjang dari vektor-vektor basis di atas adalah satu satuan.

Contoh 1:
Tentukan vektor satuan yang searah dengan vektor a→=3iˆ−4jˆ.
Penyelesaian:
Oleh karena panjang vektor a→ adalah ∣∣a→∣∣=32+(−4)2−−−−−−−−−√=25−−√=5, maka vektor satuan yang searah dengan vektor a→ adalah
aˆ===a→∣∣a→∣∣15×(3−4 )35iˆ−45jˆ 

Contoh 2:
Tentukan vektor yang searah dengan vektor a→=−3iˆ+4jˆ dan mempunyai panjang 10 satuan.
Penyelesaian:
Panjang vektor a→ adalah ∣∣a→∣∣=(−3)2+42−−−−−−−−−√=25−−√=5.
Vektor satuan yang searah dengan vektor a→ adalah
aˆ===a→∣∣a→∣∣15×(−34 )−35iˆ+45jˆ 
Dengan demikian, vektor yang searah dengan vektor a→=−3iˆ+4jˆ dan mempunyai panjang 10 satuan adalah 10aˆ=10(−35iˆ+45jˆ)=−6iˆ+8jˆ.

Contoh 3:
Diketahui titik A(2,−1) dan B(5,3). Tentukan vektor satuan yang searah dengan vektor AB−→−−.
Penyelesaian:
Vektor posisi dari titik A(2,−1) dan B(5,3) berturut-turut adalah OA−→−−=2iˆ−jˆ dan OB−→−−=5iˆ+3jˆ.

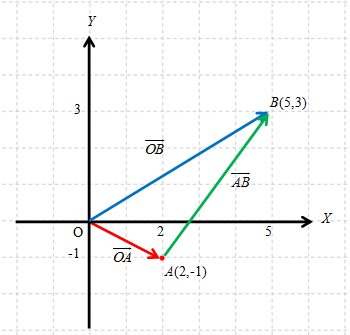
Berdasarkan gambar di atas, tampak bahwa AB−→−−=(34 )=3iˆ+4jˆ.
Dengan demikian, vektor satuan yang searah dengan vektor AB−→−− adalah
eˆ===AB−→−−∣∣AB−→−−∣∣15×(34 )35iˆ+45jˆ 

Apakah diantara kalian ada yang tahu bagaimana cara menentukan vektor pada contoh 3 di atas dengan menggunakan perhitungan?
Ya, jika kalian perhatikan anak panah pada gambar, maka akan kalian dapatkan hubungan sebagai berikut:
AB−→−−====AO−→−−+OB−→−−−OA−→−−+OB−→−−−(2−1 )+(53 )(34 ) 

Mudah bukan?

Kesamaan Dua Vektor

Vektor a→ dan b→ dikatakan sama jika dan hanya jika besar dan arahnya sama.
Misalkan a→=⎛⎝⎜klm ⎞⎠⎟ dan b→=⎛⎝⎜pqr ⎞⎠⎟.
Vektor a→ dikatakan sama dengan vektor b→ jika dan hanya jika k=p, l=q, dan m=r.
Dengan kata lain, dua buah vektor dikatakan sama apabila unsur-unsur yang bersesuaian sama.

Agar kalian semakin jelas, mari kita perhatikan contoh berikut.

Contoh 4:
Tentukan nilai x, y, dan z jika diketahui vektor a→=2iˆ+yjˆ+3kˆ dan b→=xiˆ+4jˆ+zkˆ adalah dua vektor yang sama.
Penyelesaian:
Oleh karena vektor a→ dan b→ sama, maka unsur-unsur yang bersesuaian sama.
Dengan demikian, x=2, y=4, dan z=3.