Vektor Posisi dan Panjang Vektor

November 26, 2020 No Comments

Pernahkah kalian mendengar seorang pasien yang bertanya kepada perawat tentang suhu tubuhnya?
Jawaban dari perawat tersebut tentunya adalah suatu nilai berupa besaran sebuah bilangan real. Nah, besaran tersebut selanjutnya dinamakan skalar.

Bagaimana jika seseorang mengajukan pertanyaan tentang bagaimana cara menendang bola yang benar agar masuk gawang?
Tentu saja jawabannya akan berupa perkiraan tentang besar gaya yang harus dikeluarkan untuk menendang bola serta arah tendangan bola.

Masih ingatkah kalian tentang besaran yang memiliki besar dan arah?
Ya, jawabannya adalah vektor.
Nah, dalam topik ini kalian akan belajar mengenai vektor posisi dan panjang vektor.

Konsep Dasar

Seperti yang kalian ketahui, vektor juga dapat dikatakan sebagai ruas garis berarah. Panjang ruas garis tersebut merupakan besar atau modulo atau magnitude dari suatu vektor. Adapun arah vektor ditentukan oleh arah anak panah yang menghubungkan ujung dan pangkal ruas garis.
Vektor dapat dituliskan dengan menggunakan huruf tebal, seperti a atau a→.
Kalian juga dapat menuliskan vektor melalui titik-titik yang dihubungkan oleh ruas garis, seperti AB−→−−, dimana pangkal dari vektor tersebut adalah titik A dan ujungnya adalah titik B. Nah, jika titik pangkal vektor adalah titik B dan titik ujungnya adalah titik A, maka vektor tersebut dinamakan vektor BA−→−−.

Apa yang dapat kalian simpulkan dari gambar di atas?
Ya, kedua vektor mempunyai panjang yang sama, walaupun keduanya memiliki arah yang berlawanan.
Lebih lanjut, karena vektor AB−→−− berlawanan arah dengan vektor BA−→−−, maka AB−→−−=−BA−→−−.

Vektor Posisi di R2

Apa itu vektor posisi?
Vektor posisi adalah vektor dengan titik pangkal O(0,0).
Jika P(x,y) adalah titik ujung, maka vektor OP−→−−=p→ adalah vektor posisi dari titik P(x,y) terhadap titik O(0,0).
Nah, ada tiga bentuk yang dapat kalian gunakan untuk menyatakan vektor posisi p→, yaitu:
  • vektor kolom → p→=(xy )
  • vektor baris → p→=(x,y)
  • vektor basis → p→=xiˆ+yjˆ

Yuk kita perhatikan gambar berikut agar kalian lebih jelas.

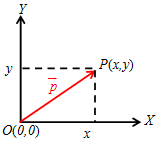
Pada gambar di atas, dapat kalian lihat bahwa komponen dari vektor posisi p→ adalah koordinat titik P(x,y).

Contoh 1:
Tentukan vektor posisi dari titik A(3,−4) dalam bentuk vektor kolom, vektor baris, dan vektor basis.
Penyelesaian:
Jika kita misalkan vektor posisi dari titik A(3,−4) adalah a→, maka
  • a→=(3−4 ) → vektor kolom
  • a→=(3,−4) → vektor baris
  • a→=3iˆ−4jˆ → vektor basis

Panjang Vektor di R2

Panjang vektor OP−→−−=p→ dengan O(0,0) dan P(x,y) dinotasikan dengan ∣∣OP−→−−∣∣=∣∣p→∣∣.

Ingatkah kalian dengan rumus jarak antara dua titik?
Ya, ∣∣OP−→−−∣∣=∣∣p→∣∣=x2+y2−−−−−−√.

Agar kalian lebih jelas, mari kita cermati dua contoh berikut.

Contoh 2:
Hitung panjang vektor OP−→−−.

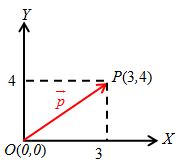
Penyelesaian:
Oleh karena vektor OP−→−− berpangkal di titik O(0,0) dan koordinat titik P adalah (3,4), maka
∣∣OP−→−−∣∣====x2+y2−−−−−−√32+42−−−−−−√25−−√5
Jadi, panjang vektor OP−→−− adalah 5 satuan.

Contoh 3:
Hitunglah panjang vektor AB−→−−.

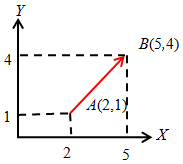
Penyelesaian:
Oleh karena vektor AB−→−− berpangkal di titik A(2,1) dan titik ujungnya adalah titik B(5,4) maka ∣∣AB−→−−∣∣====(xB−xA)2+(yB−yA)2−−−−−−−−−−−−−−−−−−−√(5−2)2+(4−1)2−−−−−−−−−−−−−−−√9+9−−−−√32√
Jadi, panjang vektor AB−→−− adalah 32√ satuan.

Nah, kalian sudah belajar tentang vektor posisi dan panjang vektor di R2.
Lalu bagaimanakah vektor posisi dan panjang vektor di R3?
Yuk kita cari tahu.

Vektor Posisi di R3

Vektor OP−→−−=p→ adalah vektor posisi dari titik P(x,y,z) terhadap titik O(0,0,0).
Sama halnya dengan vektor posisi di R2, ada tiga bentuk yang dapat kalian gunakan untuk menyatakan vektor posisi p→, yaitu:
  • vektor kolom → p→=⎛⎝⎜xyz ⎞⎠⎟
  • vektor baris → p→=(x,y,z)
  • vektor basis → p→=xiˆ+yjˆ+zjˆ

Contoh 4:
Tentukan vektor posisi dari titik A, B, C, dan D.

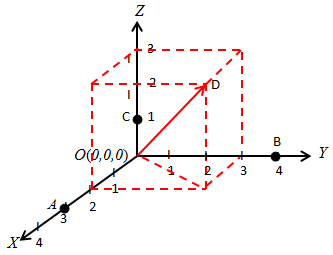
Penyelesaian:
Oleh karena A(3,0,0), B(0,4,0), C(0,0,1), dan D(2,3,3), maka vektor posisi dari titik A, B, C, dan D berturut-turut adalah
  • a→=⎛⎝⎜300 ⎞⎠⎟=3iˆ
  • b→=⎛⎝⎜040 ⎞⎠⎟=4jˆ
  • c→=⎛⎝⎜001 ⎞⎠⎟=kˆ
  • d→=⎛⎝⎜233 ⎞⎠⎟=2iˆ+3jˆ+3kˆ

Panjang Vektor di R3

Panjang vektor OP−→−−=p→ dengan O(0,0,0) dan P(x,y,z) dinotasikan dengan ∣∣OP−→−−∣∣=∣∣p→∣∣.
Panjang vektor OP−→−− di R3 juga dapat dicari dengan menggunakan rumus jarak antara dua titik, yaitu ∣∣OP−→−−∣∣=∣∣p→∣∣=x2+y2+z2−−−−−−−−−−√.
Nah, jika titik A(xA,yA,zA) dan B(xB,yB,zB), maka panjang vektor AB−→−− adalah ∣∣AB−→−−∣∣=(xB−xA)2+(yB−yA)2+(zB−zA)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√

Apakah kalian sudah paham dengan materi di atas?
Agar kalian semakin paham dengan materi di atas, mari kita perhatikan contoh berikut.

Contoh 5:
Diketahui titik A(1,1,1), B(1,2,3) dan C(3,5,2).
Tentukan panjang tiap vektor berikut: OA−→−−, OB−→−−, OC−→−−, AB−→−−, BA−→−−.
Penyelesaian:
  • ∣∣OA−→−−∣∣=12+12+12−−−−−−−−−−√=3√
  • ∣∣OB−→−−∣∣=12+22+32−−−−−−−−−−√=14−−√
  • ∣∣OC−→−−∣∣=32+52+22−−−−−−−−−−√=38−−√


∣∣AB−→−−∣∣====(xB−xA)2+(yB−yA)2+(zB−zA)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√(1−1)2+(2−1))2+(3−1)−−−−−−−−−−−−−−−−−−−−−−−√0+1+4−−−−−−−√5√


∣∣BA−→−−∣∣====(xA−xB)2+(yA−yB)2+(zA−zB)2−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√(1−1)2+(1−2))2+(1−3)−−−−−−−−−−−−−−−−−−−−−−−√0+1+4−−−−−−−√5√

Apa yang dapat kalian simpulkan tentang panjang vektor AB−→−− dan BA−→−− berdasarkan contoh di atas?
Ya, panjang vektor AB−→−− sama dengan BA−→−−.
Dengan kata lain, |AB−→−−|=|BA−→−−|.

Sekarang kalian sudah mempelajari semua materi dalam topik ini.

0 komentar:

Posting Komentar